Bivariate analyse: de uitleg en betekenis

Bivariate analyse: in dit artikel wordt de bivariate analyse praktisch uitgelegd. Het artikel begint met de definitie en betekenis van deze tool, gevolgd door een uitleg over de verschillen tussen de univariate en bivariate analyse en een praktisch voorbeeld. Je vindt ook informatie over de verschillende soorten bivariate analyse. Veel leesplezier!

Wat is een bivariate analyse?

Een bivariate analyse is een statistische methode voor het onderzoeken van de relatie tussen twee variabelen. Deze tool helpt onderzoekers bij het vaststellen van correlaties tussen twee variabelen en geeft een inzicht in de sterkte en de richting van de correlatie. Dit is gelijk het belangrijkste verschil met een univariate analyse waarbij het gaat om een grondige analyse van een enkele variable.

Deze analyse is zeer nuttig voor onderzoekers die studies uitvoeren in verschillende vakgebieden, zoals sociale wetenschappen, geneeskunde, marketing en meer.

Door het begrijpen van de bivariate analyse kunnen studenten gegevens effectief analyseren voor een onderzoek zoals een scriptie en gefundeerde conclusies trekken. In dit artikel wordt het concept van de bivariate analyse verkent en worden de voordelen ervan besproken, evenals verschillende soorten analyses met begrijpelijke uitleg en herkenbare, praktische voorbeelden.

Waarom is een bivariate analyse belangrijk?

Bivariate analyses zijn van groot belang in statistisch onderzoek. Laten we eens kijken naar enkele belangrijke redenen waarom het waardevol is:

Identificeren van trends en patronen

De bivariate analyse helpt onderzoekers verborgen trends en patronen te ontdekken door de relatie tussen twee variabelen te beoordelen.

Door de gegevens te onderzoeken, kunnen onderzoekers leren begrijpen hoe veranderingen in de ene variabele overeenkomen met veranderingen in de andere, wat waardevolle inzichten oplevert.

Voorbeeld: Bij marketingonderzoek kan bivariate analyse worden gebruikt om de relatie tussen reclame-uitgaven en verkoop te begrijpen. Door de gegevens te analyseren, kunnen onderzoekers patronen identificeren die aangeven of een toename van de reclame-uitgaven inderdaad leidt tot hogere verkoopcijfers.

Bepalen van oorzaak-en-gevolg relaties vanuit een bivariate analyse

Bivariate analyse stelt onderzoekers in staat om te beoordelen of twee variabelen statistisch met elkaar geassocieerd zijn, wat helpt bij het vaststellen van oorzaak-en-gevolg relaties.

Het helpt te bepalen of veranderingen in de ene variabele leiden tot veranderingen in de andere, of dat de relatie slechts toevallig is.

Voorbeeld: In een medisch onderzoek kan bivariate analyse worden gebruikt om de relatie tussen roken en het optreden van longkanker te onderzoeken.

Door de gegevens te analyseren, kunnen onderzoekers bepalen of er een significante associatie is tussen de twee variabelen, wat wijst op een oorzakelijk verband.

Voorspellingen doen

Bivariate analyse stelt onderzoekers in staat om voorspellingen te doen op basis van de relatie tussen twee variabelen. Door het modelleren van de relatie kunnen onderzoekers toekomstige resultaten voorspellen op basis van veranderingen in de onafhankelijke variabele.

Voorbeeld: Stel dat een onderzoeker de relatie tussen studietijd en studieresultaten wil onderzoeken. Door middel van bivariate analyse kan de onderzoeker een model ontwikkelen dat voorspelt hoe de studieresultaten veranderen naarmate de studietijd toeneemt.

Online cursus onderzoeksmethoden voor business studenten  Meer informatie

Besluitvorming

Bivariate analyse speelt een belangrijke rol bij het informeren van besluitvorming in verschillende domeinen, zoals bedrijfsleven, beleid en gezondheidszorg.

Door inzicht te krijgen in de relatie tussen twee variabelen, kunnen besluitvormers beter geïnformeerde beslissingen nemen.

Voorbeeld: In een bedrijfscontext kan een bivariate analyse worden gebruikt om de relatie tussen prijsstelling en winstgevendheid te onderzoeken. Door de gegevens te analyseren, kunnen bedrijfsmanagers bepalen welke prijsniveaus het meest gunstig zijn voor de winstgevendheid van het bedrijf.

Soorten bivariate analyse

Er zijn verschillende soorten bivariate analyse die kunnen worden gebruikt om de relatie tussen twee variabelen te onderzoeken. Hier zijn enkele van de meest voorkomende types:

Spreidingsdiagrammen

Een spreidingsdiagram is een grafiek die laat zien hoe twee variabelen met elkaar verband houden. Het toont de waarden van de ene variabele op de x-as en de waarden van de andere variabele op de y-as. Het patroon in de grafiek laat zien wat voor soort relatie er is tussen de twee variabelen en hoe sterk deze is.

Voorbeeld: Een spreidingsdiagram kan worden gebruikt om de relatie tussen leeftijd en bloeddruk te onderzoeken. Het diagram kan laten zien of er een verband is tussen hogere leeftijd en hogere bloeddruk.

Correlatieanalyse

Correlatie is een statistische maatstaf die aangeeft hoe sterk en in welke richting twee variabelen met elkaar verbonden zijn. Een positieve correlatie betekent dat wanneer de ene variabele stijgt, de andere ook stijgt. Een negatieve correlatie laat zien dat wanneer de ene variabele stijgt, de andere daalt.

Voorbeeld: Correlatie kan worden gebruikt om de relatie tussen het aantal uren studeren en de behaalde cijfers te onderzoeken. Een positieve correlatie zou betekenen dat hoe meer tijd er wordt besteed aan studeren, hoe hoger de cijfers zijn.

Regressieanalyse

Een regressieanalyse geeft toegang tot verschillende instrumenten om potentiële relaties tussen datapunten te identificeren. Het kan ook de vergelijking van de curve of lijn verschaffen, evenals de correlatiecoëfficiënt.

Voorbeeld: Regressieanalyse kan worden gebruikt om de relatie tussen de verkoopprijs van een huis en factoren zoals de grootte van het huis, het aantal slaapkamers, enzovoort te onderzoeken. Het kan helpen bij het voorspellen van de verkoopprijs op basis van deze variabelen.

Chi-kwadraattoets

De chi-kwadraattoets is een statistische methode om verschillen in één of meer categorieën tussen de verwachte en waargenomen waarden te identificeren. Onderzoekers gebruiken deze statistische test om categorische variabelen binnen dezelfde steekproefgroep te vergelijken en te valideren.

Voorbeeld: Een chi-kwadraattoets kan worden gebruikt om te bepalen of er een significant verband is tussen geslacht en politieke voorkeur in een bepaalde bevolkingsgroep.

T-toets

Een t-toets is een statistische test die de gemiddelden van twee groepen vergelijkt om te zien of er een groot verschil is. Deze analyse is geschikt wanneer je de gemiddelden van twee categorieën van een categorische variabele vergelijkt.

Voorbeeld: Een t-toets kan worden gebruikt om te bepalen of er een significant verschil is in de gemiddelde scores van mannen en vrouwen op een bepaalde toets.

Stappenplan voor het uitvoeren van een bivariate analyse

Bij het uitvoeren van een bivariate analyse zijn er enkele praktische stappen die je kunt volgen. Hier is een beknopte, eenvoudige uitleg van deze stappen:

Stap 1: gegevens verzamelen

Verzamel gegevens van de twee variabelen die je wilt analyseren. Zorg ervoor dat je voldoende gegevens hebt om een betrouwbaar resultaat te verkrijgen.

Stap 2: grafische weergaven maken

Maak een scatterplot om de relatie tussen de twee variabelen te visualiseren. Plaats de waarden van de ene variabele op de x-as en de waarden van de andere variabele op de y-as. Elk punt op de scatterplot vertegenwoordigt een gegevenspaar.

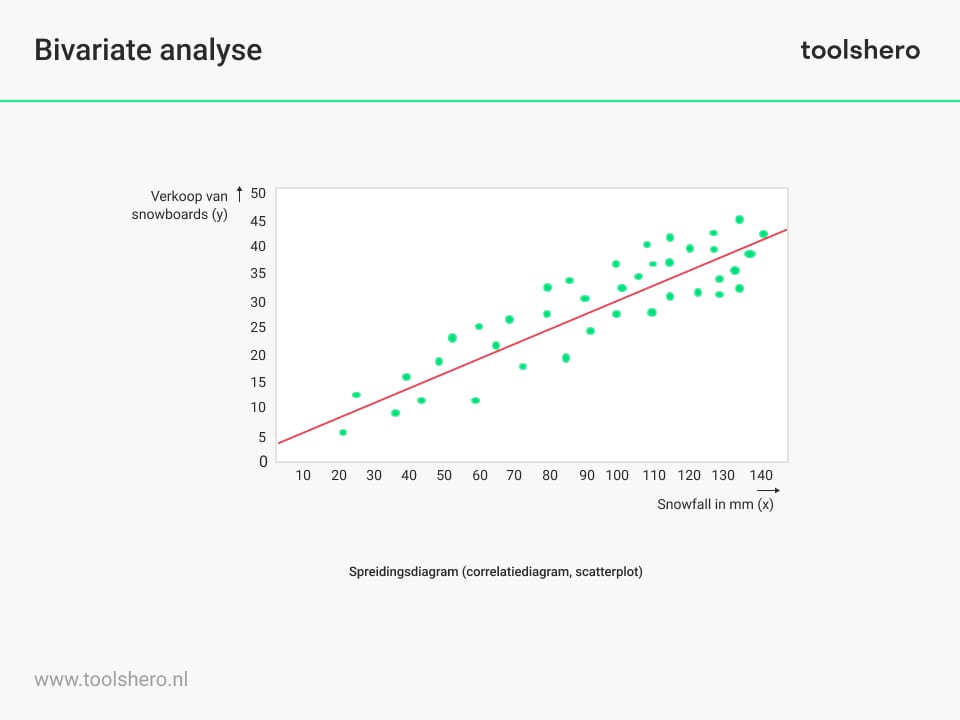
Figuur 1 – een voorbeeld van een bivariate analyse

Stap 3: correlatie beoordelen

Kijk naar de patronen op de scatterplot om te bepalen of er een correlatie bestaat tussen de variabelen. Als de punten op de scatterplot een opwaartse trend laten zien, is er sprake van een positieve correlatie.

Als de punten een neerwaartse trend vertonen, is er sprake van een negatieve correlatie. Als er geen duidelijk patroon is, is er mogelijk geen correlatie.

Stap 4: statistische methoden toepassen

Als je wilt weten hoe sterk de correlatie is, kun je een correlatiecoëfficiënt berekenen. De meest gebruikte correlatiecoëfficiënt is de zogenaamde Pearson-correlatiecoëfficiënt.

Deze varieert tussen -1 en +1, waarbij een waarde van +1 een perfecte positieve correlatie aangeeft, een waarde van -1 een perfecte negatieve correlatie aangeeft, en een waarde van 0 aangeeft dat er geen correlatie is.

Stap 5: resultaten interpreteren vanuit een bivariate analyse

Op basis van de correlatiecoëfficiënt kun je conclusies trekken over de sterkte en richting van de relatie tussen de variabelen.

Een hogere absolute waarde van de correlatiecoëfficiënt duidt op een sterkere correlatie. Let op: correlatie impliceert niet altijd causaliteit, dus wees voorzichtig bij het trekken van causale conclusies.

Bivariate analyse: de correlatie versus causaliteit

Stel je voor dat je op een dag naar buiten kijkt en ziet dat het hard regent. Je merkt op dat veel mensen buiten rondlopen met paraplu’s open. Dit is een voorbeeld van correlatie. Het lijkt erop dat wanneer het regent, mensen paraplu’s gebruiken.

Maar betekent dit dat het gebruik van een paraplu ervoor zorgt dat het regent? Of dat regen ervoor zorgt dat mensen altijd paraplu’s openen? Nee, dat is niet het geval.

Het gebruik van een paraplu is een reactie op de regen. Mensen openen hun paraplu’s om zichzelf droog te houden wanneer het regent.

Dit voorbeeld laat zien dat er een correlatie is tussen regen en het gebruik van paraplu’s. Maar het betekent niet dat het gebruik van een paraplu regen kan veroorzaken. Het is belangrijk om te begrijpen dat correlatie niet hetzelfde is als causaliteit, omdat het niet aantoont dat het ene de oorzaak is van het andere.

Om te bepalen of er causaliteit is, moeten er verder onderzoek gedaan worden. Andere factoren moeten overwogen worden en er moet gekeken worden naar verschillende situaties om te begrijpen of het gebruik van een paraplu daadwerkelijk de regen kan veroorzaken. In dit specifieke geval weten we dat het niet mogelijk is.

Nu is het jouw beurt

Wat denk jij? Herken jij de uitleg over de bivariate analyse? Had je voordat je dit artikel las al eens gehoord van de bivariate analyse? Zo ja, in welke context? Heb jij wel eens een bivariate analyse uitgevoerd? Welke grafische methoden ken jij om de relatie tussen twee variabelen weer te geven? Heb jij tips of opmerkingen?

Deel jouw kennis en ervaring via het commentaar veld onderaan dit artikel.

Meer informatie

1. Barick, R. (2021). Research Methods For Business Students. Retrieved 02/16/2024 from Udemy.
2. Bertani, A., Di Paola, G., Russo, E., & Tuzzolino, F. (2018). How to describe bivariate data. Journal of thoracic disease, 10(2), 1133.
3. Verhoeven, N. (2007). Doing research. The Hows and Whys of Applied Research. Pocket Guide to Social Work.
4. Dowdy, S., Wearden, S., & Chilko, D. (2011). Statistics for research. John Wiley & Sons.

Citatie voor dit artikel:
Janse, B. (2023). Bivariate analyse. Retrieved [insert date] from Toolshero: https://www.toolshero.nl/onderzoek/bivariate-analyse/

Oorspronkelijke publicatiedatum: 30/10/2023 | Laatste update: 21/03/2024

Wilt u linken naar dit artikel, dat kan!
<a href=”https://www.toolshero.nl/onderzoek/bivariate-analyse/”>Toolshero: Bivariate analyse</a>

Article by:

Sheryl Lynn Baas

Sheryl Lynn Baas is onze Communicatiemanager bij Toolshero en je herkent haar misschien wel van onze video's. Sheryl’s academische achtergrond ligt in de Culturele Antropologie en Ontwikkelingssociologie en ze is de oprichter van de Sheryl Lynn Foundation, een stichting voor kinderen en educatie op de Filipijnen. Ze is een manusje-van-alles en deelt verder haar gaven als spiritueel coach, presentator en DJ. Leuk weetje: Sheryl is voormalig Miss Nederland 2006.