Regressie analyse: de uitleg plus voorbeeld

Regressie analyse: in dit artikel wordt regressie analyse praktisch uitgelegd. Na het lezen zal je de basis begrijpen van deze krachtige marketingtool en methode uit de statistiek. Aan bod komt: wat deze analyse is, welke terminologie erbinnen te vinden is, wat lineaire en non-lineaire regressie analyse is en hoe de methode in de praktijk wordt gebruikt. Veel leesplezier!
Wat is een regressie analyse? De uitleg
Regressie analyse is een statistische methode die gebruikt wordt om verbanden tussen verschillende variabelen in bijvoorbeeld een dataset te vinden. Het is een belangrijk hulpmiddel voor het modelleren en analyseren van gegevens.
De techniek wordt verder gebruikt voor prognoses en het vinden van de oorzaak-gevolgrelatie. Zo wordt de techniek onder anderen gebruikt in het onderzoeken van oorzaken van dodelijke verkeersongevallen. De analyse legt de relatie bloot tussen afhankelijke variabelen en onafhankelijke variabelen. Daarnaast geeft het ook de sterkte van de impact van een variabele op een andere variabele weer.
Het is lastig om naar een grote reeks getallen in een dataset te kijken en precies te begrijpen welke relaties of associaties er tussen deze datapoints zijn. Het gebruik van een regressie analyse is dan de beste methode om een voorspelling te doen op basis van de reeks gegevens. Er zijn verschillende soorten software beschikbaar waarmee een regressie analyse kan worden uitgevoerd.
De term regressie is afgeleid van het fenomeen dat de hoogte van afstammelingen van lange voorouders de neiging hebben om korter te worden en naar het gemiddelde toe veranderen. Het werd bedacht door Francis Galton, hoewel hij het puur in de boven beschreven context bedacht. Later werd zijn werk uitgebreid voor een algemenere context. Regressie analyse blijft een belangrijk gebied van actief onderzoek. Er zijn in de afgelopen jaren veel nieuwe methoden ontwikkeld om verschillende soorten complexe regressie te identificeren.
Terminologie binnen regressie analyses
Om resultaten te ontcijferen met dezer analysevorm is het belangrijk om de basisjargon te begrijpen. De meest voorkomende terminologieën die worden gebruikt bij het uitvoeren van een regressie analyse zijn hieronder beschreven.
Relaties
Vaak wordt over correlaties gesproken in een regressie analyse, maar in feite wordt een correlatieanalyse alleen gebruikt om de relatie of associatie tussen twee continue variabelen weer te geven. Regressie analyse is een soortgelijke techniek, maar meet de relatie tussen een uitkomstvariabele en een of meerdere verstorende variabelen.
Variabelen
De uitkomstvariabele wordt ook regelmatig de respons of afhankelijke variabele genoemd. De verstorende risicofactoren worden de voorspellende of onafhankelijke variabelen genoemd. In de regressie analyse worden de afhankelijke variabelen met een Y weergeven, en worden de onafhankelijke variabelen met de letter X aangeduid.
Outliers
Uitschieters zijn een probleem in de statistiek omdat ze de meeste parametrische statistieken beïnvloeden. Onder meer gemiddelden, standaardafwijkingen en correlaties zijn daarop zeer gevoelig. Soms kunnen de uitschieters een volledige analyse waardeloos maken. Ondanks deze problemen is het niet zomaar toegestaan om de uitschieters te laten vallen. Het kunnen legitieme gegevens zijn die soms interessante oorzaken kunnen hebben. Het is daarom belangrijk om de oorzaak van de uitschieters te vinden.
Multicollineariteit
Er wordt van multicollineariteit gesproken als de onafhankelijke variabelen correlaties blijken te hebben in deze analysevorm. Dit kan een probleem zijn omdat onafhankelijke variabelen onafhankelijk horen te zijn. Het idee is dat wanneer de waarde wordt gewijzigd van een bepaalde onafhankelijke variabele, een andere onafhankelijke variabele gelijk blijft.
Geeft een wijziging in de ene een wijziging door aan de andere, dan wordt het moeilijk voor het model om de relatie tussen onafhankelijke variabelen en de afhankelijke variabelen in te schatten. Dat komt omdat beide variabelen de neiging hebben om gelijktijdig veranderd te worden.
Heteroscedasticiteit / homoscedasticiteit
Homoscedasticiteit is wanneer de foutterm, een ruis of andere verstoring, gelijk is voor alle waarden van de onafhankelijke variabele. Heteroscedasticiteit is aanwezig wanneer de grootte van deze foutterm verschilt tussen bepaalde waarden van een onafhankelijke variabele.
Regressie analyse: lineaire regressie
Lineaire regressie is een vorm van een analyse waarbij de relatie geanalyseerd wordt tussen afhankelijke variabelen (Y) en een of meerdere onafhankelijke variabelen (X). Dit wordt gevisualiseerd door een lijn, bekend als de regressielijn. De aard van de lijn is lineair, zoals de naam doet vermoeden. In deze vorm is de afhankelijke variabele continue, en de onafhankelijke variabele kan continu of onderbrekend zijn.
Dit is de eenvoudigste vorm van een analyse. Zo kan er bijvoorbeeld eenvoudig worden aangegeven wat de relatie is tussen de kilometerstand van een auto is en de onderhoudskosten.

Figuur 1 – Lineaire regressie analyse voorbeeld
Regressie analyse: non-lineair Regression Analysis
Het kenmerkende van een lineaire variant van deze analyse is dat de lijn lineair is. Een niet-lineaire vergelijking kan dus vele verschillende vormen aannemen. Hierom biedt deze vorm van een regressie analyse ook de beste functionaliteiten voor curve-fitting. . Onder niet-lineaire regressie vallen meerdere types, waaronder de onderstaande.
Logistic regression
Logistische regression is de vorm van een regressie analyse die gebruikt wordt om de dichotome afhankelijke uitkomstvariabele te linken aan een of meerdere andere variabelen. Het is een voorspellende analysetool en wordt gebruikt om de relatie tussen de ene en de andere variabele te beschrijven. Dit type regressie analyse ligt het dichtstbij lineaire analyse en kan gezien worden als een alternatief voor lineaire analyse als de gemeten variabelen niet continu zijn.
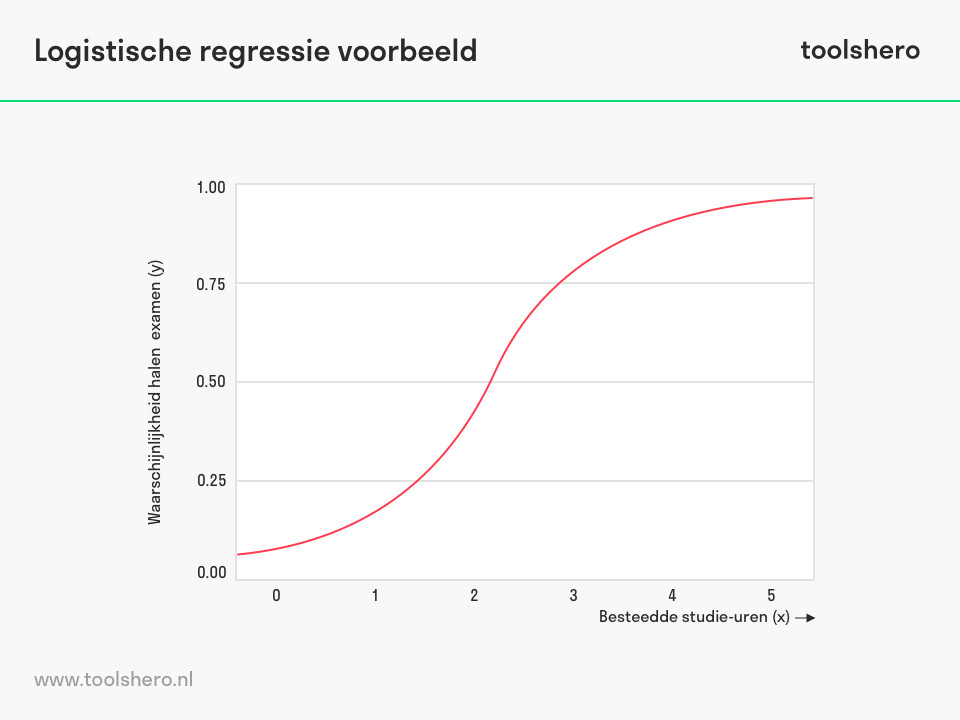
Figuur 2 – Logistische regressie analyse voorbeeld
Ridge Regression
Eerder zagen we al dat datasets te kampen hebben met meerdere problemen zoals multicollineariteit. In het geval van multicollineariteit kunnen de regressiegegevens alsnog geanalyseerd worden met speciale types analyse zoals de Ridge Regression. De formule reduceert de standaardfouten in de variabelen en zo hoopt men dat de resultaten betrouwbaarder zullen worden.
Lasso Regression
Lasso Regression is een type van regressie analyse waarbij gebruik wordt gemaakt van krimpen. Krimpen treedt op wanneer regressiecoëfficiënten worden gekrompen en naar een centraal punt gebracht worden, zoals het gemiddelde of 0. Dit type regressieanalyse is geschikt voor datasets met een hoog niveau van multicollineariteit. Het acroniem LASSO staat voor Least Absolute Shrimping and Selection Operator.
Regressie analyse in de praktijk
Deze analysevorm is voor iedereen uit te voeren die hulp kan gebruiken bij het vinden van relaties in gegevens. Ook voor zakelijke beslissingen blijkt de regressie analyse een effectieve hulptool.
Het kan helpen bij het bestuderen van gegevens en relaties weergeven die een ondernemer kan helpen bij het voorspellen van de verkoop op korte of lange termijn, of hoe de voorraadniveaus er uit zullen zien in de toekomst. De analysetool kan ook gebruikt worden om de vraag en aanbood naar een product of service uit een industrie beter te begrijpen. Hoe meer data hoe meer verschillende variabelen invloed zouden kunnen hebben op deze dingen.
Voor prognoses wordt de regressie analyse gebruikt om de relatie tussen twee verschillende variabelen weer te geven, de afhankelijke en onafhankelijke variabelen. Zo kan er een relatie vastgesteld worden tussen het BBP (bruto binnenlands product) en de omzet van een bedrijf en antwoord worden gegeven op de vraag: als het BBP met 3% stijgt, hoe veel kan mijn omzet dan stijgen?
Nu is het jouw beurt
Wat denk jij? Herken jij de uitleg over de regressie analyse? Werk jij wel eens met deze vorm van data-analyse, of denk jij dat het toegepast kan worden in jouw werkomgeving? Heb jij tips of aanvullingen?
Deel jouw kennis en ervaring via het commentaar veld onderaan dit artikel.
Meer informatie
- Draper, N. R., & Smith, H. (2014). Applied regression analysis (Vol. 326). John Wiley & Sons.
- Montgomery, D. C., Peck, E. A., & Vining, G. G. (2012). Introduction to linear regression analysis (Vol. 821). John Wiley & Sons.
- Watson, G. S. (1964). Smooth regression analysis. Sankhyā: The Indian Journal of Statistics, Series A, 359-372.
Citatie voor dit artikel:
Janse, B. (2019). Regressie analyse. Retrieved [insert date] from Toolshero: https://www.toolshero.nl/marketing-modellen/regressie-analyse/
Oorspronkelijke publicatiedatum: 09/11/2019 | Laatste update: 18/05/2023
Wilt u linken naar dit artikel, dat kan!
<a href=”https://www.toolshero.nl/marketing-modellen/regressie-analyse/”>Toolshero: Regressie analyse</a>






