Moderne portefeuilletheorie van Harry Markowitz

Moderne portefeuilletheorie: dit artikel geeft een praktische uitleg van de Modern Portfolio Theory (MPT) van Harry Markowitz. Het artikel begint met een algemene definitie van de moderne portefeuilletheorie, gevolgd door voorbeelden van de basisformule en de stappen die nodig zijn om een ​​portefeuille te beoordelen. Vervolgens worden specifieke kenmerken uitgelegd en vind je enkele praktische tips om dit model te gebruiken. Veel plezier met lezen!

Wat is de moderne portefeuilletheorie?

De moderne portefeuilletheorie, ook bekend als de Modern Portfolio Theory (MPT), is een economisch raamwerk waarmee beleggers minimale marktrisico’s proberen te nemen en maximaal rendement behalen voor een bepaalde beleggingsportefeuille.

In de theorie wordt benadrukt dat risico inherent is aan een hogere opbrengst, en dat het niet voldoende is om naar het verwachte risico en rendement van een enkel aandeel te kijken.

Door in meer dan een enkel aandeel te beleggen kan een investeerder beter profiteren van de voordelen van diversificatie, door middel van een vermindering in risicovolle aandelen.

Het risico van afzonderlijke aandelen is hoger dan het risico van aandelen in een gecombineerde portefeuille, op voorwaarde dat de risico’s van die verschillende aandelen niet een direct verband houden.

Zie daarom de moderne portefeuille als een methode waarin twee soorten risicovolle aandelen meegenomen zijn: een die winst levert als het regent, en een ander die winst levert als het niet regent. Een portefeuille die beide soorten aandelen bevat zal altijd vruchten afwerpen.

De moderne portefeuilletheorie werd voorgesteld door econoom Harry Markowitz in een essay uit 1952. Later kreeg hij hiervoor een Nobelprijs voor de economie.

Het verband tussen risico en verwacht rendement

De moderne portefeuilletheorie gaat ervan uit dat investeerders risicomijdend zijn.

Dat betekent dat zij een portefeuille met minder risico verkiezen boven een riskante portefeuille met een bepaald rendementsniveau. Een belegger neemt alleen meer risico als het verwachte rendement hoger is.

Het verwachte rendement van een gecombineerde set aandelen, de portefeuille, wordt berekend als een gewogen som van het rendement van de individuele aandelen. Stel een portefeuille bestaat uit 5 aandelen met een verwacht rendement van 3, 6, 9, 12 en 15%, dan is de som voor het berekenen van het gemiddelde verwachte rendement:

Verwachte rendement = (3% x 20%) + (6% x 20%) + (9% x 20%) + (12% x 20%) + (15% x 20%)

Risico-opbrengstverhouding

De risico-opbrengstverhouding verwijst naar de potentiële beloning die een investeerder of belegger kan verdienen voor elke euro die geïnvesteerd wordt.

Veel investeerders gebruiken de risico-opbrengstverhouding op te beslissen of zij hun gewenste rendement kunnen behalen met een investering.

Een investering met een risico-opbrengstverhouding van 1:5 suggereert dat een investeerders bereid is om 1 euro te investeren met het vooruitzicht om 5 euro te verdienen. Een risico-opbrengstverhouding van 1:3 geeft aan dat een investeerder verwacht om 3 euro te verdienen op zijn investering van 1 euro.

Handelen gebruiken deze benadering om de juiste transacties op het goede moment te plannen. De verhouding wordt berekend door het bedrag dat verloren kan worden door een onverwachte nieuwe koers, te delen door de hoeveelheid winst die handelen verwachten te maken wanneer de positie wordt gesloten.

Bij het beoordelen van de geschiktheid van aandelen door beleggers wordt vaak 1:3 verwacht rendement gezien als ideaal. Dat betekent dat zij drie eenheden rendement verwachten voor elke eenheid extra risico.

Beleggers gebruiken verschillende tools om de risico-opbrengstverhouding binnen de perken te houden, zoals stop-loss orders en putopties.

Een stop-loss order is een handelstrigger die de verkoop van een aandeel uit een bepaalde portefeuille automatiseert als het aandeel een specifiek dieptepunt heeft bereikt.

Een putoptie is een contract dat de investeerder het recht geeft om een bepaald bedrag van een onderliggend waardepapier te verkopen tegen een vooraf bepaalde prijs binnen een bepaald tijdsbestek.

Diversificatie in de beleggersportefeuille

Een populair gezegde in de beleggerswereld is ‘niet al je eieren in één mandje leggen’. Hieruit kan worden afgeleid dat beleggers adviseren om niet al het kapitaal in één bedrijf, index of ander gebied te investeren.

Dat adviseren zij omdat het risico dat het volledig kapitaal verloren gaat bij een crisis groot is. In plaats daarvan adviseren beleggers om te kijken naar een verscheidenheid aan investeringen die variëren als het gaat over rendement en risico.

Dat proces van risicospreiding wordt diversificatie genoemd, en is de leidende gedachte achter de moderne portefeuilletheorie. Verschillende studies hebben aangetoond dat diversificatie voor 25% minder portefeuillerisico kan zorgen.

Correlatie tussen investeringen

Elke investering heeft gevolgen voor het rendement en risico van de hele portefeuille. De eerste stap bij het beoordelen van deze portefeuille is het bepalen van de verwachte waarde van het toekomstige rendement van de investering.

De tweede stap is om te focussen op het fluctuatiebereik van het rendement omdat beleggersontwikkelingen kunnen afwijken van de verwachtingen. Daarbij wordt gekeken naar de standaarddeviatie van de verwachte opbrengsten. Dat helpt bij het bepalen van uitschieters in beide richtingen.

Daarna moet worden vastgesteld of er een onderlinge samenhang is tussen investeringen. Dat wordt correlatie genoemd. Correlatie heeft een waarde van tussen de 1 en -1. Als een investering niet reageert op de waarde schommeling van een andere investering, correleren zij niet en is de correlatiewaarde gelijk aan 0.

Indien een waarde schommeling van een aandeel niet altijd reageert op de waarde schommeling van een ander aandeel is de correlatie zwak en dichterbij 0.

Investeringen en onderlinge waarde schommelingen kunnen ook een negatieve correlatie hebben. In dat geval leidt een waardestijging van een aandeel tot een lagere waarde van een ander aandeel.

Voorbeeld positieve en negatieve correlatie tussen investeringen

Een voorbeeld van een positieve correlatie tussen aandelen of opties is de prijs voor ruwe olie en de aandelen van grote oliemaatschappijen.

Wanneer de olieprijs stijgt, dan zullen de aandelen van deze oliemaatschappijen ook stijgen. Dalen de olieprijzen, dan neemt ook de waarde van de aandelen van de oliemaatschappij af.

Dat komt omdat hun omzet en winst minder wordt als gevolg van de lagere verkoopprijs van een vat ruwe olie.

Een ander voorbeeld is de prijscorrelatie tussen goud en zilver. Beide zijn edelmetalen, alternatieve beleggingsobjecten. De prijs van zilver stijgt als de prijs van goud stijgt, en vice versa.

Een voorbeeld van een negatieve correlatie tussen aandelen of opties is de relatie tussen nationale aandelenindexen, en de prijs van goud. Wanneer een nationale aandelenindex stijgt, daalt de goudprijs meestal. Dat komt omdat goud wordt beschouwd als een veilige haven om geld op te slaan.

Wanneer de aandelenindex stijgt, wenden beleggers zich vaker tot goud. Zij verkopen hun aandelen in goud wanneer de traditionele aandelen in een stroomversnelling omhoog zitten om te profiteren van de opleving.

Kenmerken van de moderne portefeuilletheorie

Een portefeuille met aandelen die alleen positief correlerende beleggingen bij elkaar houdt negeert de basisprincipes van diversificatie en is waarschijnlijk niet bestand tegen een crisis.

Als alle investeringen met elkaar in verband staan vallen zij dus allemaal tegelijk in slechtere tijden. Het verlies van een specifieke groep aandelen wordt dus niet gecompenseerd door een groep aandelen die in waarde stijgt.

Doorgaans proberen beleggers zoveel mogelijk balans in de portefeuille aan te brengen. Volgens de bedenker van de moderne portefeuilletheorie is een efficiënte portefeuille een reeks investeringen die maximaal rendement kan behalen tegen het laagst mogelijke risico dat de belegger wil en kan nemen.

Groepen aandelen worden onder gebracht in risicogroepen. Een goede portefeuille bestaat uit aandelen van meerdere groepen. Een mogelijke classificatie van deze groepen is als volgt:

Risicogroep 1

Dit zijn stabiele en veilige beleggingsopties. Het gaat hierbij om:

• Spaarboeken
• Europese geldmarktfondsen
• Contant geld
• Deposito’s met een vaste looptijd

Risicogroep 2

Dit zijn conservatieve beleggingsopties. Hieronder vallen:

• Effecten met vaste rente
• Obligaties met hoge kredietwaardigheid
• Pensioenfondsen
• Geldmarkt gerelateerde fondsen
• Risicovrije staatsobligaties

Risicogroep 3

Dit zijn beleggingsopties die gericht zijn op solide winstgevendheid. Hieronder vallen onder meer:

• Aandelen van gevestigde bedrijven
• Aandelenfondsen met standaardwaarden
• Internationale vastrentende waarden
• Aandelen en gemengde fondsen

Risicogroep 4

Een hogere risicogroep zijn beleggingsopties waarop gespeculeerd wordt over de winst. Het gaat hierbij om:

• Aandelen en aandelenfondsen met standaardwaarden
• Obligaties met gemiddelde ratings
• Obligaties in vreemde valuta
• Beleggingsfondsen

Risicogroep 5

De hoogste risicogroep zijn beleggingsopties waarop veel gespeculeerd wordt. Hieronder vallen:

• Hoog speculatieve obligaties
• Leningen
• Futures
• Junk bonds
• Andere staatsobligaties

Volgens de moderne portefeuilletheorie heeft elke risicogroep zijn eigen efficiënte portefeuille. Deze verschillen veel in samenstelling, en zijn als het ware een weerspiegeling van de risicotolerantie van de belegger.

Aan de ene kant van het spectrum bevinden zich de zeer speculatieve beleggingsportefeuilles, en aan de andere kant de op veiligheid gerichte portefeuille. Daar tussenin zijn er efficiënte portefeuilles met gemengde beleggingen.

Efficient Frontier

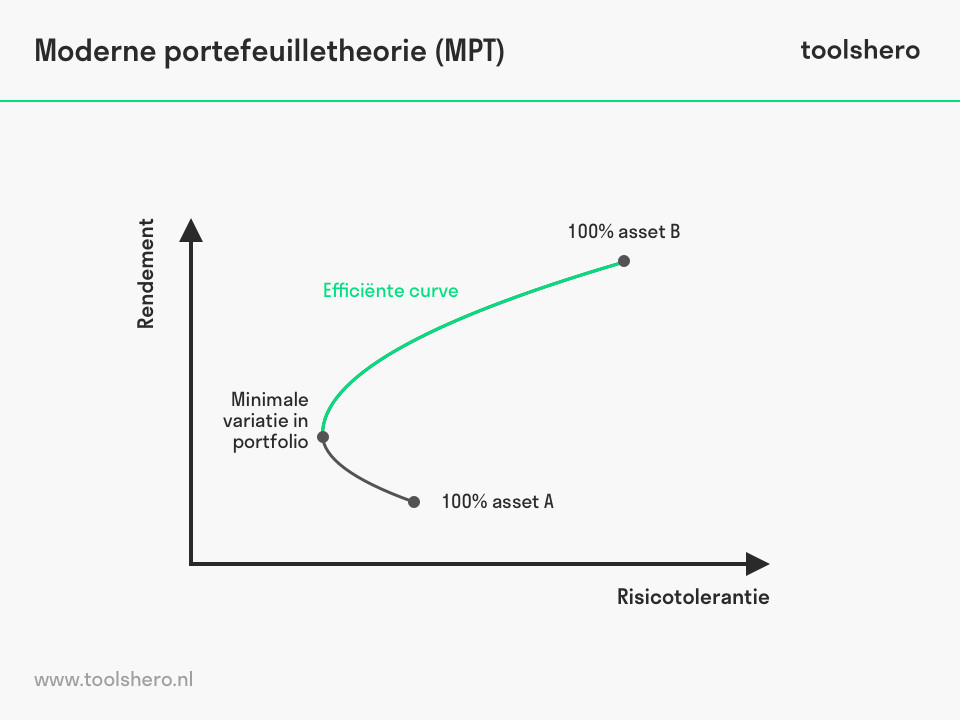
Figuur 1 – Figuur 1 – Voorbeeld van de moderne portefeuilletheorie

De efficiënte grens beoordeelt portefeuilles op een schaal van rendement versus risico. Het rendement wordt over de y-as weergegeven, en het daaraan hangende risico op de y-as.

Een beleggingsportefeuille binnen de efficiënte grens is een set van optimale beleggingsopties die het hoogste verwachte rendement bieden voor een bepaald risiconiveau.

Portefeuilles die onder de efficiënte grens liggen zijn niet optimaal omdat zij onvoldoende rendement opleveren voor het risiconiveau wat er aan vast hangt. Portefeuilles die rechts van de efficiënte grens geclusterd worden zijn ook niet optimaal omdat zij een hoger risiconiveau hebben voor het verwachte rendement.

De theorie achter de efficiënte grens (efficiënt frontier) werd evenals de moderne portefeuilletheorie ook geïntroduceerd door Harry Markowitz, en is een hoeksteen van deze portefeuilletheorie.

Hoe komt de efficient frontier tot stand?

De efficiënte grens vertegenwoordigt op een grafische manier portefeuilles die het rendement maximaliseren voor een verondersteld risico.

Rendement is afhankelijk van de beleggingscombinaties binnen een bepaalde portefeuille. De standaarddeviatie van een beleggingsoptie is gelijk aan het risico.

In het meest ideale geval probeert de belegger zijn portefeuille te vullen met opties die uitzonderlijke rendementen bieden, maar waarvan de gecombineerde standaarddeviatie lager is dan de standaarddeviatie van een individuele optie. Als de mix van deze opties ideaal is, zal de portefeuille langs de efficiënte grenslijn geplaatst worden.

De kromming van de efficiënte grenslijn komt door de diversificatie van beleggingsopties. De kromming maakt duidelijk hoe diversificatie het risico-opbrengstniveau van de portefeuille verbetert. Het laat verder zien dat er een afnemend marginaal risico is. De relatie tussen risico en opbrengst is niet lineair.

Met andere woorden, het toevoegen van meer risico aan een bepaalde portefeuille zal niet hetzelfde aan rendement opleveren. Optimale portefeuilles hebben doorgaans een hoge mate van diversificatie dan portefeuilles die niet optimaal zijn.

Moderne portefeuilletheorie samenvatting

De moderne portefeuilletheorie is geïntroduceerd door Harry Markowitz, en dient als een raamwerk voor beleggers om een optimale beleggingsportefeuille samen te stellen.

De theorie stelt dat risico en opbrengst onlosmakelijk met elkaar verbonden is, en dat het draait om een combinatie van aandelen met een hoger risico/rendement, en aandelen met lager risico en rendement.

Beleggers adviseren om een verscheidenheid aan investeringen op te nemen in een bepaalde portefeuille die variëren als het gaat over rendement en risico. Dat proces van risicospreiding wordt diversificatie genoemd, en is de leidende gedachte achter de Moderne portefeuilletheorie.

Daarna moet worden vastgesteld of er een onderlinge samenhang is tussen investeringen. Dat wordt correlatie genoemd.

Correlatie heeft een waarde van tussen de 1 en -1. Een voorbeeld van een positieve correlatie tussen beleggingsopties is de prijs van ruwe olie en de waarde van de aandelen van grote oliemaatschappijen.

Als de olieprijs stijgt, wordt de waarde van deze bedrijven groter en zullen de aandelen ook in waarde stijgen.

Indien een portefeuille bestaat uit een efficiënte combinatie van beleggingsopties komt deze op de efficiënt frontier te liggen. Dat is een grafische representatie van een veilige en moderne beleggingsportefeuille.

Nu is het jouw beurt

Wat denk jij? Herken jij de uitleg over de moderne portefeuilletheorie (Modern Portfolio Theory (MPT))? Pas jij de moderne portefeuilletheorie toe wanneer jij belegt? Welke tips kan jij met ons delen over het spreiden van risico in beleggingen? Heb tips of opmerkingen?

Deel jouw kennis en ervaring via het commentaar veld onderaan dit artikel.

Meer informatie

1. Haugen, R. A., & Haugen, R. A. (2001). Modern investment theory (Vol. 5). Upper Saddle River, NJ: Prentice Hall.
2. Markowitz, H. M. (1991). Foundations of portfolio theory. The journal of finance, 46(2), 469-477.
3. Markowitz, H. M. (2010). Portfolio theory: as I still see it. Annu. Rev. Financ. Econ., 2(1), 1-23.

Citatie voor dit artikel:
Janse, B. (2020). Moderne portefeuilletheorie (Markowitz). Retrieved [insert date] from toolshero: https://www.toolshero.nl/strategie/moderne-portefeuilletheorie/

Oorspronkelijke publicatiedatum: 16/12/2020 | Laatste update: 16/01/2024

Wilt u linken naar dit artikel, dat kan!
<a href=”https://www.toolshero.nl/strategie/moderne-portefeuilletheorie/”>toolshero: Moderne portefeuilletheorie (Markowitz)</a>

Article by:

Ben Janse

Ben Janse is een young professional en werkzaam als Content Manager bij Toolshero. Daarnaast houdt hij zich binnen zijn studie International Business aan de Hogeschool Rotterdam bezig met het analyseren en ontwikkelen van managementmodellen. Dankzij zijn theoretische en praktische kennis weet hij hoofd- en bijzaken goed te onderscheiden waardoor de essentie van elk artikel goed naar voren komt.