Speltheorie: de uitleg plus een voorbeeld

Speltheorie: in dit artikel wordt het concept van de speltheorie, ook bekend als Game Theory praktisch uitgelegd. Naast de uitleg wat het is, behandelt dit artikel ook de Speltheorie economie, het rationeel handelen, de hoofdtakken, de opbrengstenmatrix en een uitgewerkt praktisch speltheorie voorbeeld. Na het lezen begrijp je de basis van deze krachtige strategie en besluitvorming tool. Veel leesplezier!

Wat is speltheorie? De uitleg

Speltheorie is een kansberekening techniek om situaties met strategische interacties tussen verschillende beslissingsnemers te analyseren en de uitkomst van hun genomen beslissingen te voorspellen.

Voornamelijk voor bedrijven die bijvoorbeeld willen toetreden op een nieuwe markt met bepaalde producten of hun prijs ten opzichte van de concurrent willen verlagen om zo een groter marktaandeel te creëren, is de speltheorie een mogelijkheid om te kijken welke beslissing het beste zal zijn.

Het gaat erom welke keuzes een deelnemer voor handen heeft en hoe die genomen keuze beïnvloed wordt door de keuze van andere deelnemers.

Er wordt gesproken van een Nash evenwicht wanneer het voor geen enkele speler voordelig is om van een strategieprofiel af te wijken als andere spelers dat ook niet doen.

Speltheorie economie

De speltheorie is een tak van de wiskunde en werd in 1944 beschreven in het boek theory of games and economic behaviour door de econoom Oskar Morgenstern en de wiskundige John von Neumann.

Vanuit de basis is de speltheorie ontstaan uit de analyse van beslissingen die genomen worden bij het spelen van bordspellen; hier dankt het zijn naam ook aan.

Uiteindelijk is de speltheorie, door toepassing vanuit andere disciplines, uitgegroeid tot een onderdeel van de wetenschap. Aan de hand van modellen wordt geprobeerd om de keuzes van deelnemers beter te begrijpen en te kijken wat voor invloed dat heeft op elkaars beslissingen.

Speltheorie : Rationeel handelen

De speltheorie gaat er vanuit dat mensen rationeel handelen. Daaruit vloeit voort dat deelnemers hun genomen beslissing op zijn minst net zulke gelijke kans geven als de mogelijk andere alternatieven.

Dat heeft met een gedeelte in de hersenen te maken dat de ‘decision maker’ heet. Bij de nadering van een druk kruispunt, doet deze ‘decision maker’ aan een razendsnelle kansberekening, voordat de beslissing wordt genomen het kruispunt wel of niet over te steken.

Zo werkt ook de speltheorie; het is een mathematische rationalisatie die zich bij iedereen afspeelt op het moment dat men een beslissing neemt. Elk menselijk handelen, gaat vooraf aan rationele afwegingen die worden gemaakt op basis van een aantal opties.

Aan de hand hiervan kunnen de ‘spellen’ binnen de speltheorie in verschillende categorieën worden verdeeld, waardoor de meest optimale uitkomst van een spel kan worden gevonden. De uitkomst van een spel kan vervolgens weer belangrijk inzicht geven in het nemen van (bedrijfs)beslissingen.

Hoofdtakken

Binnen de speltheorie gelden twee hoofdtakken; de coöperatieve en niet-coöperatieve speltheorie. Het verschil tussen deze twee typen spellen is dat er vooraf bij coöperatieve spellen bindende afspraken tussen de deelnemers gemaakt kunnen worden, terwijl dit niet mogelijk is bij de niet coöperatieve spellen.

Daarnaast zijn er nog andere takken, die nauw verbonden zijn met de speltheorie, waaronder de Beslissingstheorie. Dit is een onderdeel van de coöperatieve speltheorie die zich richt op het een persoonsspel van één deelnemer.

Het wordt vaak gebruikt in de vorm van een beslissingsanalyse, die aantoont wat de beste keuze is, op basis van informatie die vooraf is ingewonnen. De nadruk ligt op voorkeuren en overtuigingen.

Opbrengstenmatrix

Met behulp van een zogenoemd simultaan spel, kan er met de speltheorie gekeken worden wat de beste beslissing is, als de deelnemers gelijktijdig en zonder dat zij weten wat de ander doet, hun actie bepalen.

Een opbrengstenmatrix brengt dan visueel de opbrengst van elke deelnemer in beeld, bij alle mogelijke combinaties en beslissingen.

Per deelnemer kan er dan gekeken worden wat de beste beslissing is, als de andere partij kiest voor beslissing x; dit wordt ook wel de ‘best respons-methode’ genoemd. Die (voorlopig) beste keuze wordt in de opbrengstenmatrix onderstreept.

Vervolgens maakt de deelnemer die horizontaal vermeld staat (de rijspeler) een keuze:

• als de deelnemer die in de verticale kolom kiest voor beslissing 1, kan de rijspeler het beste kiezen voor beslissing 2
• als de deelnemer die in de verticale kolom kiest voor beslissing 2, kan de rijspeler het beste kiezen voor beslissing 2

De deelnemer die verticaal vermeld staat (de kolomspeler) maakt ook een keuze:

• als de rijspeler kiest voor beslissing 1, kan de kolomspeler het beste kiezen voor beslissing 2
• als de rijspeler kiest voor beslissing 2, kan de kolomspeler het beste kiezen voor beslissing 2

Er wordt gesproken van een dominantie strategie wanneer een deelnemer eenzijdig kiest voor dezelfde beslissing als de ander, ongeacht wat de keuze van die ander ook zal zijn.

Een uitgewerkt Speltheorie voorbeeld

Stel dat Dylan en Maria werken bij een projectorganisatie. Elk project is gemoeid met veel geld. Het is daarom goed om vooraf te bekijken of het lucratief is om met een nieuwe project te starten. Daar zijn veel factoren mee gemoeid, die in getallen worden uitgedrukt in onderstaande matrix.

Dylan is speler 1 en is tevens de rijspeler. Het gaat erom te onderzoeken, wat de meest dominante strategie voor Dylan is. Maria is speler 2 en tevens de kolomspeler. Haar keuzes zijn bepalend voor wat Dylan uiteindelijk gaat doen.

Beiden hebben de keuze om met een project te ‘starten’ of te ‘stoppen’ en hun belangrijkheid om voor één van beide te kiezen, wordt in cijfers uitgedrukt. Het eerste cijfer is van speler 1 (Dylan) en het 2e cijfer is van speler 2 (Maria).

Nu kun je je afvragen wat er gebeurt met Dylan, als Maria kiest om te starten met het project? -> Dylan scoort een 1 als ook hij gaat starten, maar een 2 als hij wil stoppen. Omdat 2 een hogere score is dan 1, kiest Dylan in dit geval om te stoppen.
Wat gebeurt er met Dylan als Maria kiest om te stoppen met het project? -> Dylan scoort -1 als hij gaat starten met het project, maar een 2 als hij gaat stoppen. Omdat 2 een hogere score is dan -1, zal hij in dat geval ook kiezen voor stoppen.
Ongeacht of Maria gaat starten of stoppen met het project, is het voor Dylan het beste om te stoppen. Dit is zijn meest dominante strategie.

Desalniettemin kunnen we ook naar Maria haar strategie kijken. Wat gebeurt er met Maria als Dylan kiest om te starten met het project? -> Maria scoort een 1 als zij ook gaat starten, maar -3 als zij wil stoppen. Omdat 1 hoger is dan -3, zal zij ervoor kiezen om te starten.
Wat gebeurt er met Maria als Dylan kiest om te stoppen met het project? -> Maria scoort -1 als zij ook gaat starten en een 3 als zij ook gaat stoppen. Omdat 3 hoger is dan 1, zal zij in dat geval kiezen om te stoppen.

Stoppen met het project is dus voor beiden de beste strategie. Omdat Maria de 2e speler is, is haar strategie minder dominant en is het Dylan die als eerste de meest dominante strategie gaat toepassen. Hij kiest er ongetwijfeld voor om te stoppen met het project.

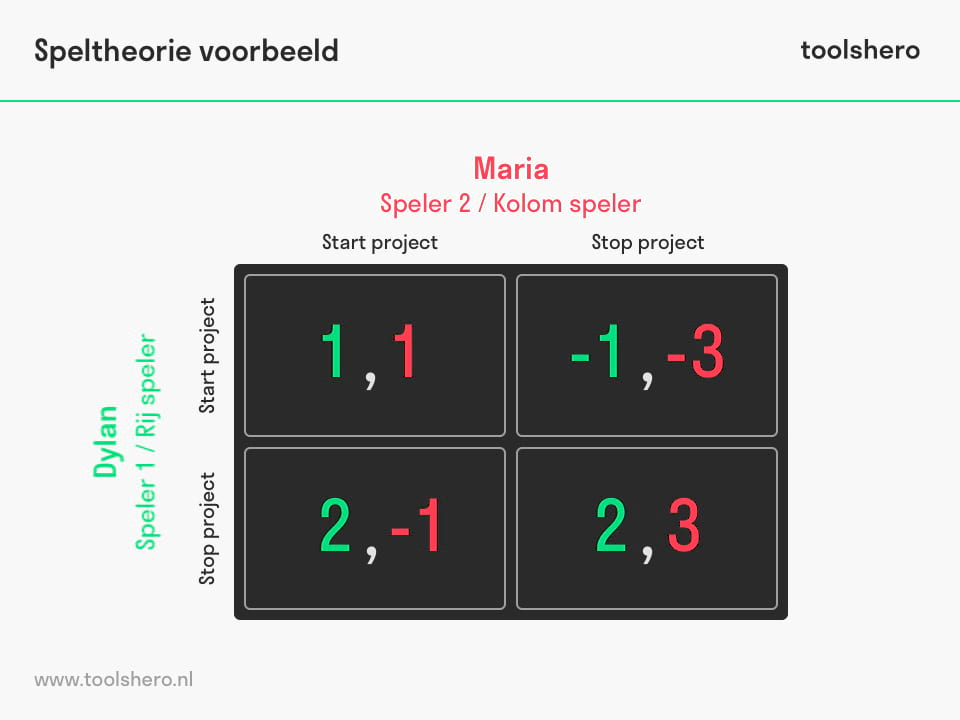
Figuur 1 – een uitgewerkt voorbeeld van de speltheorie

Sequentieel spel

Het kan ook voorkomen dat de beide deelnemers na elkaar een keuze maken. Dit heet de sequentiële of simultane speltheorie. Degene die als eerste een beslissing neemt heeft wellicht het voordeel, maar moet wel rekening houden met alle mogelijke reacties van de andere deelnemer.

Bij sequentiële spellen zijn de deelnemers zich bewust van de acties van de andere deelnemers bij hun beslissing. In de meeste gevallen wordt bij sequentieel spel gebruik gemaakt van een beslisboom, waarmee alle mogelijke combinaties van acties in kaart worden gebracht.

Daardoor wordt het inzichtelijk voor een bedrijf om wel of niet aan prijsverhoging te doen en zo ja, hoe hoog de prijsverhoging moet zijn om de concurrent voor te blijven.

De speltheorie levert veel mogelijkheden op, die kunnen sturen in het nemen van belangrijke strategische beslissingen. Desalniettemin blijft het een kansberekening die niet volledig berust op feiten, maar op mogelijkheden die zich voor zouden kunnen doen.

Door vooraf genoeg en juiste informatie te verzamelen, kan met behulp van de speltheorie een redelijk goede prognose worden gesteld. Mocht de werkelijkheid echter anders uitpakken, dan is dat realiteit en zullen de deelnemers vroegtijdig acties moeten ondernemen om hun beslissing bij te sturen.

Nu is het jouw beurt

Wat denk jij? Wat is jouw ervaring met de speltheorie? Herken het bovenstaande of heb je aanvullingen? Wat zijn volgens jou andere succesfactoren die bij kunnen dragen aan goede strategisch besluitvorming?

Deel jouw kennis en ervaring via het commentaar veld onderaan dit artikel.

Meer informatie

1. Morgenstern, O. (1976). The collaboration between Oskar Morgenstern and John von Neumann on the theory of games. Journal of Economic Literature, 14(3), 805-816.
2. Morgenstern, O. & Von Neumann, J. (2007, 1944). Theory of games and economic behavior. Princeton University Press.
3. Weintraub, E. R. (Ed.). (1992). Toward a history of game theory (Vol. 24). Duke University Press.

Citatie voor dit artikel:
Mulder, P. (2018). Speltheorie. Retrieved [insert date] from Toolshero: https://www.toolshero.nl/strategie/speltheorie/

Oorspronkelijke publicatiedatum: 13/02/2018 | Laatstw update: 11/04/2023

Wilt u linken naar dit artikel, dat kan!
<a href=”https://www.toolshero.nl/strategie/speltheorie/”>Toolshero: Speltheorie</a>

Article by:

Patty Mulder

Patty Mulder is een management expert op het gebied van competentie ontwikkeling, time management, persoonlijke effectiviteit en zakelijke communicatie. Naast content schrijven, is ze een business coach en verzorgt ze bedrijfstrainingen.