Multicriteria analyse (MCA)

Multicriteria analyse: in dit artikel wordt de Multicriteria analyse (MCA) praktisch uitgelegd. Dit artikel bevat een uitgebreide uitleg van MDCDA, de stappen die daarbij komen kijken en een voorbeeld. Na het lezen begrijpt u de noodzaak en de voordelen van risicoanalyse. Veel plezier met lezen!
Wat is een Multicriteria analyse (MCA)?
Een Multiple Criteria Decision Analysis (MCDA), of Multicriteria analyse (MCA), is een beslissingsanalyse die meerdere (conflicterende) criteria in de besluitvorming evalueert. De tool wordt gebruikt door vrijwel iedereen in het dagelijks leven, een mens neemt duizenden beslissingen op een dag, maar ook in andere omgevingen zoals het bedrijfsleven, overheidsinstanties en medische centra.
Een Multicriteria analyse (MCA) lijkt op een kosten-batenanalyse, maar heeft als voordeel dat niet enkel monetaire eenheden vergeleken kunnen worden. Bij het maken van veelomvattende of belangrijke beslissingen dient er rekening te worden gehouden met meerdere criteria of maatstaven.
Het vergelijken van tegenstrijdige criteria, zoals kwaliteit en kosten, kan soms onduidelijk en verwarrend zijn. Het nemen van een beslissing gebaseerd op meerdere criteria met behulp van de multicriteria analyse kan dan duidelijkheid verschaffen. Door het structureren van complexe problemen en het analyseren van meerdere criteria worden er beter geïnformeerde en gerechtvaardigdere beslissingen genomen.
Stanley Zionts publiceerde in 1979 een artikel met de naam ‘MCDM – If not a Roman numeral, then what?’. Daarmee populariseerde en promootte hij het concept bij zijn ondernemerspubliek. In de jaren daarna bleef de tool voor besluitvorming populair en zijn er meerdere MCA-gerelateerde organisaties opgericht zoals de ‘International Society on Multi-criteria Decision Making’.
In een uitgebreide Multicriteria analyse (MCA) wordt kennis gebruikt uit verschillende gebieden, waaronder: wiskunde, economie, informatietechnologie, software engineering, en andere informatie systemen.
De stappen uitgelegd in een multicriteria analyse voorbeeld
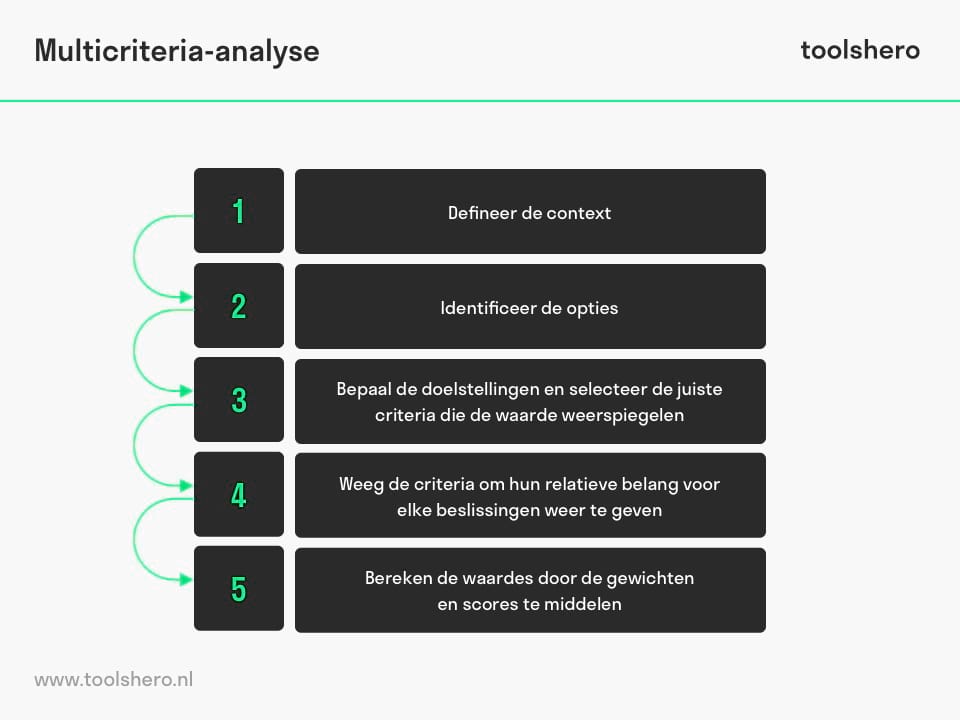
Figuur 1 – de stappen voor het uitvoeren van een multicriteria analyse
1. Definieer de context
Voordat er aan de slag kan worden gegaan met een multicriteria analyse moet aan de context duidelijk vorm worden gegeven. De context houdt rekening met de huidige situatie, sleutelspelers en belanghebbenden in de besluitvorming. Voordelen van een heldere contextbeschrijving zijn:
- De beste allocatie van verschillende middelen om de doelstellingen te bereiken
- Verbeterde communicatie tussen verschillende partijen
- Faciliteren van meerdere nieuwe opties
- Het in kaart brengen van zwakke en sterke punten, kansen en dreigingen. Een handige tool die hiervoor gebruikt kan worden is de SWOT analyse
- Het erkennen en mogelijk uitsluiten van onzekerheden in de omgeving waarin de analyse wordt uitgevoerd. Een PEST analyse helpt hierbij.
2. Identificeer de opties
In een multicriteria analyse worden meerdere opties tegen elkaar afgewogen. Of de opties vooraf zijn opgesteld of dat deze nog ontwikkeld moeten worden, ze zijn allemaal vatbaar voor verandering en beïnvloeding. Daarom moeten de opties, terwijl de analyse al gestart is, aangepast kunnen worden. Vaak worden de opties geformuleerd op een go/no-go basis.
Of er een go of een no-go besluit wordt genomen hangt af van de consequenties die zijn verbonden aan elke optie.
3. Bepaal de doelstellingen en selecteer de juiste criteria die de waarde weerspiegelen
De consequenties spelen een centrale rol in de multicriteria analyse.
Omdat er verschillende consequenties zijn voor verschillende opties, bijvoorbeeld een hogere Return on Investment (ROI) na een investering of een verslechterde kwaliteit van producten na aanpassingen in de productielijn, moeten er verschillende criteria worden vastgesteld.
Criteria zijn duidelijke maatstaven om de effecten van opties te vergelijken en drukken de waarde uit die de verschillende opties creëren.
Bij het kopen van een auto wil de toekomstige eigenaar mogelijk kosten minimaliseren en voordelen maximaliseren. De kosten zijn makkelijk te vergelijken maar aan voordelen kunnen verschillende interpretaties worden gegeven.
Deze twee doelstellingen zijn daarom tegenstrijdig en niet direct te vergelijken. De voordelen dienen dan onderverdeeld te worden in, wanneer mogelijk, meetbare criteria zoals veiligheid (crashtest beoordeling), comfort, luxe, betrouwbaarheid en prestaties.
Het beslissen over criteria in een multicriteria analyse is dan ook vaak een kwestie van oordelen. Niet altijd is een objectieve meting mogelijk.
4. Weeg de criteria om hun relatieve belang voor elke beslissingen weer te geven
Alleen het selecteren van de juiste criteria is niet genoeg om de voorkeursschalen te combineren en analyseren. Een voorkeurseenheid is niet noodzakelijkerwijs gelijk aan een andere voorkeurseenheid.
Hetzelfde gebeurt met het vergelijken van twee temperatuurschalen zoals Celsius en Fahrenheit. Beide schalen geven de temperatuur aan, maar 1 graad Celsius verschil zorgt voor meer temperatuurverschil dan 1 graad Fahrenheit.
Het effect hiervan, het relatieve belang, merkt ook de autokoper wanneer hij een keuze moet maken tussen verschillende auto’s. De koper kan zijn keuze deels laten afhangen van de kosten die deze auto met zich meebrengt.
Maar wanneer hij een shortlist heeft gemaakt van pakweg vijf auto’s die hij graag zou willen hebben, en deze auto’s verschillen allemaal 150 euro in prijs, is dit criterium niet meer erg belangrijk. Echter, was het verschil tussen deze auto’s 3000 euro, dan zou de koper dit criterium mogelijk meer gewicht geven.
Het gewicht van een criterium geeft dus zowel het verschil aan tussen de opties en hoeveel dat verschil ertoe doet. De koper kan dus aan bijvoorbeeld veiligheid een lager gewicht geven dan aan onderhoudskosten omdat hij dit minder belangrijk vindt.
5. Bereken de waardes door de gewichten en scores te middelen
In de voorlaatste stap wordt de algemene voorkeursscore berekend. De algemene voorkeursscore is het gewogen gemiddelde van alle criteria. Eerst moeten de scores voor elk criterium vermenigvuldigd worden met het gewicht, uitgedrukt in decimalen (e.g. 20 als 0.2). Daarna worden alle scores voor elk criterium bij elkaar opgeteld. De som hiervan is de voorkeursscore. Zie voorbeeld hieronder.
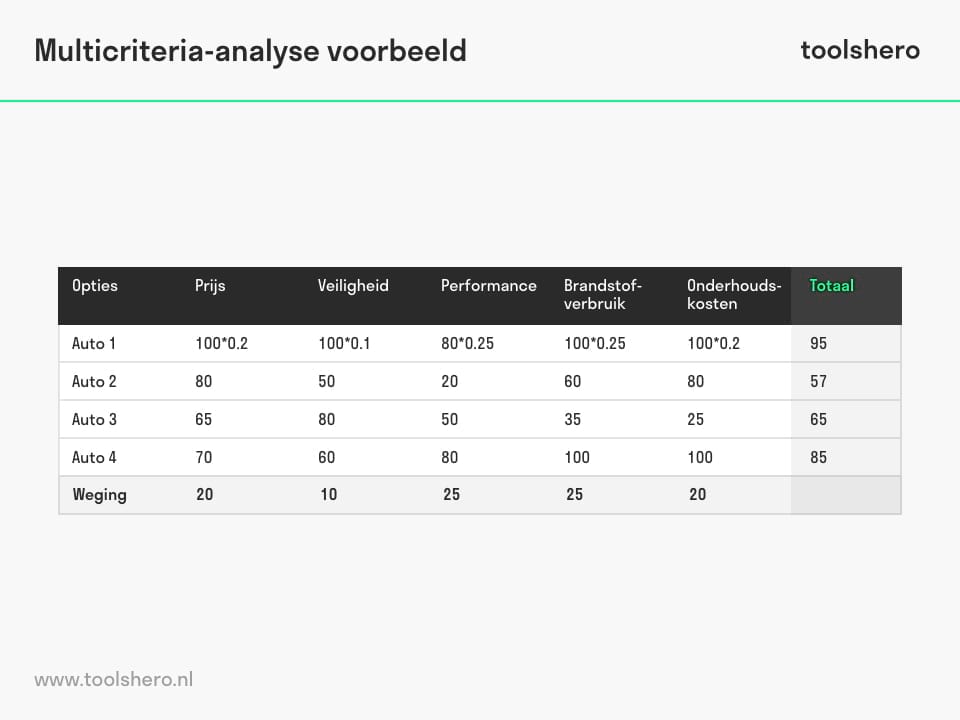
Figuur 2 – Multicriteria analyse voorbeeld uitwerking
Na het berekenen van de totaalscores kunnen de uitkomsten gerangschikt worden om te zien welke optie het meest geschikt is op basis van de toegekende voorkeursscores.
In dit voorbeeld is auto 1 de beste keuze. Belangrijk om hierbij te vermelden is dat een hoge score op bijvoorbeeld de prijs niet aangeeft dat de auto duur is, maar juist past binnen het budget van de koper.
Indien de auto erg duur is wordt een lage score gegeven aan het criterium prijs met als gevolg dat de totaalscore ook lager wordt.
Multicriteria analyse voordelen
Het gebruik van een multicriteria analyse heeft verschillende voordelen ten opzichte van een besluitvorming tool die niet gebaseerd is op specifieke criteria:
- Het is open en expliciet
- De keuze van criteria kan worden aangepast
- Veel actoren kunnen worden vergeleken
- Een Multicriteria analyse (MCA) geeft inzicht in het effect van verschillende waardeoordelen
- Prestatiemetingen kunnen worden uitbesteed aan experts
- Scores en gewichten kunnen worden gebruikt als controlemiddel
- Het is een belangrijk communicatiemiddel voor de verschillende partijen die meebeslissen over een bepaalde keuze
Nu is het jouw beurt
Wat denk jij? Herken jij de uitleg over de Multicriteria analyse (MCA)? Wat zijn volgens jou zaken die bijdragen aan de effectiviteit van dit krachtige, formele en analytische instrument voor de besluitvormer?
Deel jouw kennis en ervaring via het commentaar veld onderaan dit artikel.
Meer informatie
- Zionts, S. (1979). MCDM—if not a roman numeral, then what?. Interfaces, 9(4), 94-101.
- Zeleny, M., & Cochrane, J. L. (1973). Multiple criteria decision making. University of South Carolina Press.
- Masud, A. S., & Ravindran, A. R. (2008). Multiple criteria decision making. CRC Press, An imprint of the Taylor and Francis Group.
- Habenicht, W., Scheubrein, B., & Scheubrein, R. (2002). Multiple criteria decision making. Theme, 6(5).
Citatie voor dit artikel:
Janse, B. (2018). Multicriteria analyse (MCA). Retrieved [insert date] from Toolshero: https://www.toolshero.nl/besluitvorming/multicriteria-analyse-mca/
Oorspronkelijke publicatiedatum: 21/01/2018 | Laatste update: 09/08/2023
Wilt u linken naar dit artikel, dat kan!
<a href=”https://www.toolshero.nl/besluitvorming/multicriteria-analyse-mca/>Toolshero: Multicriteria analyse (MCA)</a>













4 reacties op “Multicriteria analyse (MCA)”
In mijn MCA heb ik met + en – gewerkt. nu moet hier een score (waarde) aan toegekend worden. Moet ik ook op 100 uitkomen? Maar kan dit? Ik snap het niet goed. Kan iemand mij helpen?
Hoi Sanne, bedankt voor je vraag. Bij het toekennen van de scores voor de criteria van jouw opties hoef je niet op 100 uit te komen. Het is de bedoeling dat je ergens tussen 0-100 een waarde toekent afhankelijk van hoe de optie presteert op het door jou gestelde criterium. In het voorbeeld zie je dat aan auto 1 een score van 100 is toegekend aan het criterium ‘veiligheid’. Dit betekent dat auto 1 de veiligste is van allemaal.
Vervolgens vermenigvuldig je de toegekende waarde met het gewicht van het criterium als decimaal getal. In het voorbeeld is aan veiligheid een gewicht van 10 (0.1) gegeven. Omdat het totaal van de wegingen 100 is, betekent dit concreet dat veiligheid 10% van de beslissing beïnvloed. Ook het totaal van de wegingen hoeft geen 100 te zijn. Als je elk criterium op dezelfde manier berekend, en alle scores optelt, is de optie met de hoogste voorkeursscore jouw beste optie.
Als je verder nog vragen hebt horen wij dat graag. Succes met je analyse!
De uitleg dat het prijscriterium bij grote prijsverschillen meer gewicht zou moeten krijgen dan bij kleine prijsverschillen deugt volgens mij niet. Het belang van een criterium is voor de eindbeslissing score*weegfactor. Waarom zou je als de score veel verschilt dit nog eens willen vergroten door de weegfactor ervoor ook nog te vergroten? Het zou betekenen dat als je 4 opties hebt met ongeveer de zelfde prijs je zou werken met een laag gewicht voor prijs, maar zodra je een vijfde goedkope of juist dure optie toevoegt dit gewicht zou vergroten. Een robuust beoordelingskader is niet van elastiek.
Dank je wel voor je aanvullende reactie, Hans