Borda count methode: de uitleg

Borda count methode: in dit artikel wordt de Borda count methode praktisch uitgelegd. Naast wat het is, belicht dit artikel een concreet rekenvoorbeeld en de oplossing, de kritiek en de alternatieven. Na het lezen begrijpt u de basisprincipes van dit krachtige besluitvormingshulpmiddel. Veel plezier met lezen!

Wat is de Borda count methode? De uitleg

De Borda count methode is een eenvoudige tool die gebruikt wordt bij verkiezingen en in de besluitvorming in verschillende hedendaagse situaties.

Aan elke kandidaat wordt een aantal punten gegeven, en zodra alle stemmen geteld zijn is de optie met de meeste punten de beste, en dus de winnaar.

Deze methode is bedoeld om verschillende opties en kandidaten te kunnen kiezen, in plaats van de optie die wordt geprefereerd door de meerderheid. Het wordt om deze reden ook wel beschreven als een op consensus gebaseerd stemsysteem. De tegenpool hiervan is het majoriteit-systeem.

De Borda count methode werd onafhankelijk van elkaar op verschillende momenten in het verleden ontwikkeld. Als eerste werd het rekenhulpmiddel ontwikkeld door Ramon Llull in de dertiende eeuw. Het was echter de Franse wiskundige en marine-ingenieur Jean-Charles de Borda naar wie de tool vernoemd werd.

Hij bedacht het systeem in 1770. Tegenwoordig wordt het als stemsysteem bijvoorbeeld nog gebruikt om leden van het parlement van Nauru te kiezen.

Ook in het democratische Slovenië wordt de Borda count methode nog actief gebruikt. Buiten de parlementsgebouwen wordt de tool wereldwijd gebruikt door verschillende organisaties en wedstrijdorganisatoren.

Rekenvoorbeeld Borda count methode

Bij de Borda count methode worden punten gegeven aan elke keuze op basis van de rangorde. Hierbij krijgt de laagste plek 1 punt, en elke opeenvolgende plek op de lijst krijgt een extra punt.

De eerste plek wordt dus beloond met 4 punten als er 4 opties zijn. Mathematisch krijgt de eerste positie dus N punten, de tweede N-1, de derde N-2, en de vierde N-3, enz.

In het rekenvoorbeeld komt een groep van 100 astrofysici bij elkaar voor een jaarlijkse conferentie. Zij wonen verdeeld over het Europese continent dichtbij de steden Budapest, Amsterdam, Oslo en Sevilla.

Om te beslissen waar de conferentie gehouden wordt besluiten zij om de Borda count methode te gebruiken, om te stemmen over de meest geschikte locatie. De resultaten van de stemming wordt hieronder in de tabel weergegeven.

Figuur 1 – Voorbeeld van Borda Count-methode

De 100 stembiljetten zijn ingezameld, en er wordt gestart met het daadwerkelijk tellen van de stemmen. In de tabel hierboven zien we dat 53 stembiljetten Amsterdam als voorkeursstad hebben. Amsterdam krijgt daarom N punten (4). Amsterdam wordt gevolgd door Oslo (N-1), Budapest (N-2) en Sevilla (N-3).

Rekenvoorbeeld oplossing

Als de hierboven uitgelegde regels toegepast worden op alle stembiljetten, is het resultaat een overzicht met de hoeveelheid punten per optie.

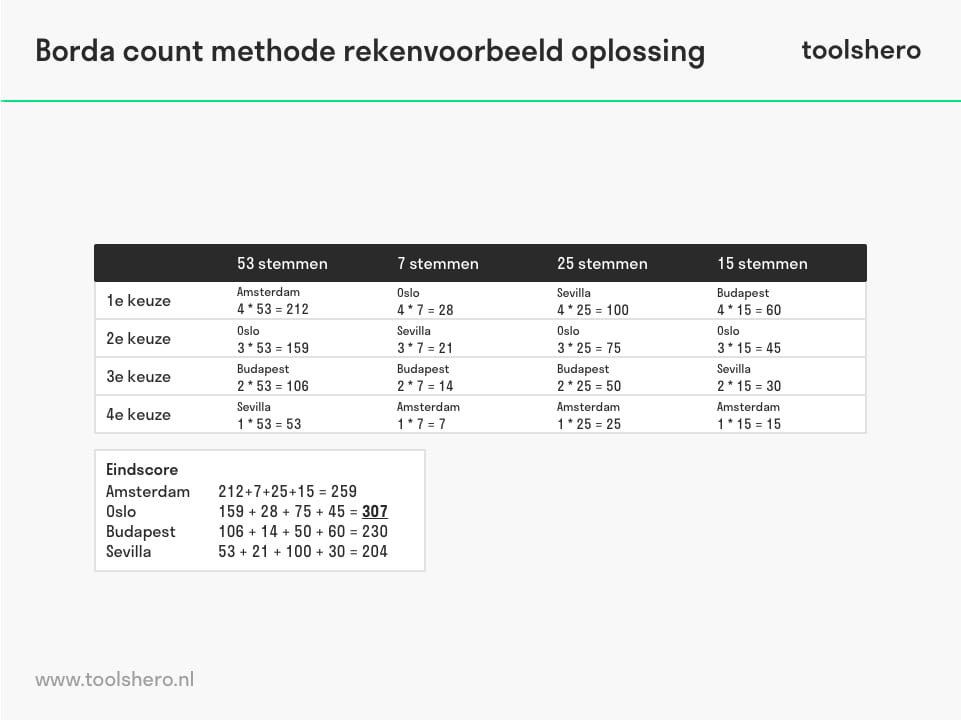
Figuur 2 – Voorbeeld plus oplossing Borda count methode

Als alle punten bij elkaar worden opgeteld is de eindscore als volgt:

Amsterdam: 212 + 7 + 25 + 15 = 259
Oslo: 159 + 28 + 75 + 45 = 307
Budapest: 106 + 14 + 50 + 60 = 230
Sevilla: 53 + 21 + 100 + 30 = 204

Als de Borda count methode doorslaggevend is voor de keuze van een conferentiestad, is Oslo de winnaar van deze stemming.

Kritiek op de Borda count methode

In het voorbeeld hierboven valt op dat Amsterdam de meeste eerste keus stemmen had, maar ondanks dat wint Oslo de stemronde. Dat gaat regelrecht tegen het principe in dat de wil van de meerderheid geschiede.

Hoewel 51 procent van de astrofysici aangaf graag naar Amsterdam te willen komen, is Oslo de stad die uit de berekening komt. Dat komt door compromissen. De Borda count methode is een op consensus gebaseerd stemsysteem, en in het voorbeeld is Oslo de locatie waarvoor de honderd wetenschappers de minste concessies hoeven doen.

Compromissen zetten echter ook de deur open voor manipulatie en tactisch stemmen.

Manipulatie

Kiezers kunnen invloed uitoefenen op de uitkomst door onoprecht de positie van de eerste keus kandidaat te verslechteren ten opzichte van de tweede keus kandidaat. Ook kunnen zij een voorkeurskandidaat helpen door de positie van de tweede keus kandidaat te verslechteren op het stembiljet.

Om deze reden liet de Franse Academie van de Wetenschappen, waarvan Borda lid was, het systeem gaan. Een reden daarvoor was dat zij ontdekten dat ook andere mensen wisten hoe zij de Borda-regel konden manipuleren.

Zij konden hun grote vijanden onderaan de lijst zetten, en daarmee veel kandidaten buiten spel zetten. In antwoord op dit kritiekpunt zei de bedenker van het systeem: ‘Mijn schema is alleen voor eerlijke mannen’.

Borda count methode alternatieven

Meervoudsstelsel

Dit wordt ook wel ‘the winner takes all’ genoemd. Hierbij wordt de zetel simpelweg gegeven aan de persoon die de meeste stemmen heeft ontvangen bij de verkiezing. De kandidaat hoeft daarvoor niet meer dan vijftig procent van de stemmen te hebben, maar moet alleen meer stemmen hebben dan de andere kandidaten.

Deze pluraliteitssystemen vertegenwoordigen echter niet als de Borda count methode de belangen van de meeste kiezers. Onder andere in de Amerikaanse politiek wordt het pluraliteitssysteem gebruikt.

Meerderheidsstelsel

In dit kiesstelsel wordt geprobeerd een grote mate van representativiteit te bieden door te eisen dat kandidaten een meerderheid van de stemmen moeten halen. Met een meerderheid wordt meer dan vijftig procent bedoeld. Als geen kandidaat dat voor elkaar krijgt, wordt er een tweede ronde gehouden.

In deze tweede ronde mogen slechts enkelen uit de eerste ronde deelnemen. Er zijn verschillende variaties op dit systeem. In Rusland gaan bijvoorbeeld de twee grootste door naar de tweede ronde. In Frankrijk gaan alle kandidaten met een minimum percentage van 12.5 procent van de stemmend oor naar de tweede ronde.

Samenvattend

Jean-Charles de Borda bedacht in de dertiende eeuw een methode om stemmingen te faciliteren in de politiek. In dit systeem worden punten gegeven aan meerdere opties. De optie met de meeste 1^e keus stemmen krijgt N punten. Elke daaropvolgende optie krijgt 1 punt minder.

Uiteindelijk worden de punten opgeteld voor elke optie, en wint de optie met de meeste punten de stemming. Hierdoor kan het voorkomen dat zelfs de optie met meer dan 50 procent van alle voorkeursstemmen het niet haalt. Om deze reden heeft de organisatie achter de methode, de Franse Academie voor de Wetenschap, de methode laten varen.

Andere stemsystemen die gebruikt worden zijn de meervoudsstelsel en meerderheidsstelsels. Deze zijn minder vatbaar voor manipulatie, zoals het geven van onoprechte stemmen.

Nu is het jouw beurt

Wat denk jij? Herken jij de uitleg over de Borda count methode? Kun jij dit hulpmiddel voor tellen gebruiken in jouw omgeving? Welke andere rekentools ken jij? En welk systeem is minder vatbaar voor manipulatie en fraude? Heb jij tips of opmerkingen?

Deel jouw kennis en ervaring via het commentaar veld onderaan dit artikel.

Meer informatie over de Borda count methode

1. Black, D. (1976). Partial justification of the Borda count. Public Choice, 28(1), 1-15.
2. Lansdowne, Z. F., & Woodward, B. S. (1996). Applying the borda ranking method. Air Force Journal of Logistics, 20(2), 27-29.
3. Lumini, A., & Nanni, L. (2006). Detector of image orientation based on Borda Count. Pattern Recognition Letters, 27(3), 180-186.
4. Ratliff, T. C. (2002). A comparison of Dodgson’s method and the Borda count. Economic Theory, 20(2), 357-372.

Citatie voor dit artikel:
Janse, B. (2019). Borda count methode. Retrieved [insert date] from Toolshero: https://www.toolshero.nl/besluitvorming/borda-count-methode/

Oorspronkelijke publicatiedatum: 21/01/2018 | Laatste update: 25/03/2024

Wilt u linken naar dit artikel, dat kan!
<a href=”https://www.toolshero.nl/besluitvorming/borda-count-methode/”>Toolshero: Borda count methode</a>

Article by:

Ben Janse

Ben Janse is een young professional en werkzaam als Content Manager bij Toolshero. Daarnaast houdt hij zich binnen zijn studie International Business aan de Hogeschool Rotterdam bezig met het analyseren en ontwikkelen van managementmodellen. Dankzij zijn theoretische en praktische kennis weet hij hoofd- en bijzaken goed te onderscheiden waardoor de essentie van elk artikel goed naar voren komt.